启发式算法2

阅读数: 次 2021-08-07

本篇介绍模拟退火算法的同时，同时引入一下机器学习中的玻尔兹曼机和逻辑斯蒂回归

首先我们要先考虑热平衡这一现象，它一般指的是温度在时间或空间上的稳定。而物理退火过程，是指在降温的物体，温度越低，能量越低，够低后，物体内部开始结晶，此时能量状态最低；而退火就是缓慢的降温，在每个温度都达到平衡态，最后在常温达到基态。人们试图参考这个过程的机理，来构造一种算法。

首先热平衡时，物理学中证明了，一个粒子系统处于各种状态的概率服从玻尔兹曼分布：

$F\left( state \right) =k\exp \left( -\frac{E}{kT} \right)$

这里$E$是状态能量，$k$的玻尔兹曼常数，$T$是温度。再由统计学规律，该系统呈现特定状态的概率为：

$p_i=\frac{\exp \left( -E_i/kT \right)}{\sum\nolimits_{j=1}^M{\exp \left( -E_j/kT \right)}}$

那么可以得出，两个不同状态的概率之比仅与能量有关：

$\frac{p_i}{p_j}=\frac{\exp \left( -E_i/kT \right)}{\exp \left( -E_j/kT \right)}$

上面的推导说明，固体降温时，同一个温度，分子停留在能量小的状态的概率大于停留在能量大的状态的概率，温度越高，不同能量状态对应的概率相差越小，随着温度越来越低，能量明显高于当前状态的粒子会越来越少，最终绝大多数分子稳定了下来，

如果我们将，物理退火时的，物体的内部状态，看作要求解的问题的解空间，状态能量看作解的好坏，状态能量越低，说明越是我们要找的解，而温度类比成一个控制状态能量迁移的参数。那么退火过程就是随着控制参数的逐渐变化，解在解空间内也开始变化，最后当控制参数停止时，即“能量最低状态”，得到的就是“最优解”。

也就是，它允许以一定的概率接受劣化解，使得搜索的过程中有更多的可能，这个规则被称为：Metropolis准则

$p\left( T \right) =\left\{ \begin{array}{c} 1,\varDelta f\geqslant 0\\ e^{-\varDelta f/\left( kT \right)},\varDelta f<0\\ \end{array} \right.$

那么模拟退火算法其实就是，我们从某个点开始进行随机扰动，如果随机出的结果更好，那么就选择它，如果随机出的效果不好，那么就以上面所说的概率进行判定，从而决定是选择还是不选择，下面我们举几个例子：

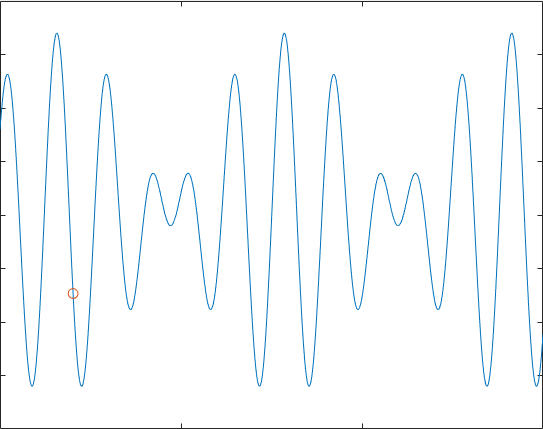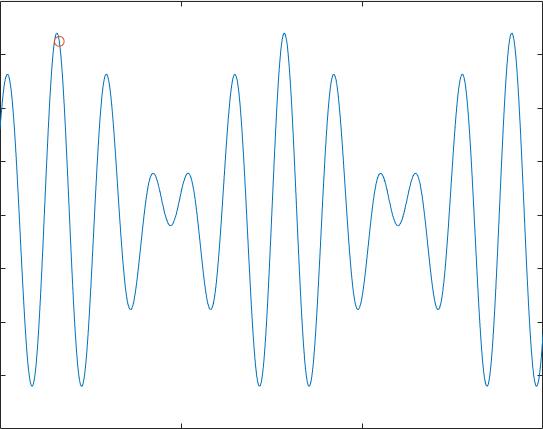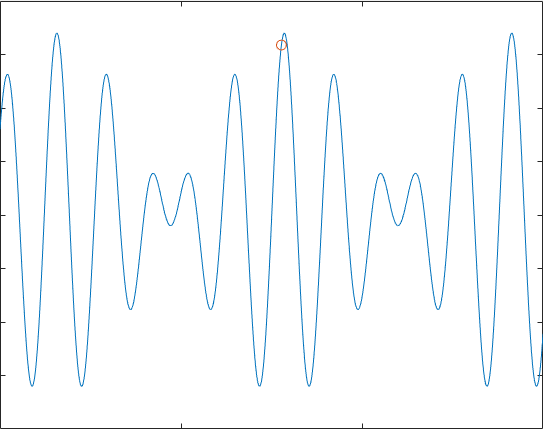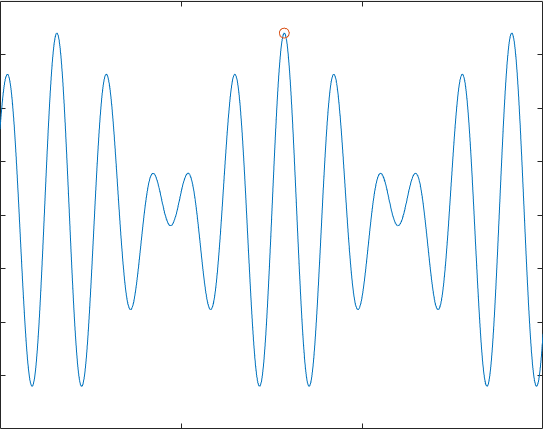
计算$f(x)=9sin(5x)+8cos(4x),，x\in \left[ 0,15 \right]$的最大值。

这里的用matlab的编程实现要比之前的遗传算法简洁的多：

clear all
clc

X=0:0.01:15;
Y=val(X);
n=1;

x_max=15;
x_min=0;
%初始温度，停止温度与降温系数
temp=1e2;
temp_min=1e-3;
alpha=0.98;

%生成初始随机解
x_old=(x_max-x_min)*rand();
x_new=x_old;
y_old=val(x_old);
y_new=y_old;

text_temp=text(0,0,'Init');

while(temp>temp_min)
  %随机扰动
  delta=(rand()-0.5)*3;
  x_new =x_old+delta;
  %扰动的值出界时，进行纠正
  if x_new<x_min || x_new>x_max
    x_new = x_new - 2 * delta;
  end
  y_new=val(x_new);
  %求差值，由于我们求最大值，所以这里dE<0是y_old-y_new
  dE=y_old-y_new;
  flag=judge(dE,temp);
  if(flag)
    x_old=x_new;
    y_old=y_new;
  end        
  %只有当dE < 0的情况下才降温
  if(dE < 0)
    delete(text_temp);
    plot(X,Y);
    hold on
    scatter(x_old,y_old);
    text_temp=text(0.3, 21, ['temp: ', num2str(temp)]);
    hold off
    f=getframe;%捕获坐标区或图窗作为影片帧
    [I,map] = rgb2ind(f.cdata,256,'nodither');
      if n==1
         imwrite(I,map,'videos.gif','DelayTime',0,'LoopCount',inf)
         n=0;
      else   
         imwrite(I,map,'videos.gif','gif','WriteMode','append','DelayTime',0);
      end
    %上面是绘图的代码，下面降温
    temp=temp *alpha;
  end

这里用到的两个定义的子函数是：

function y=val(x)
    y=9*sin(5*x)+8*cos(4*x);
end

function flag=judge(dE,t)
  if(dE<0)
    flag=1;
  else
    p=exp(-(dE/t));
    if(p>rand)
      flag=1;
    else
      flag=0;
    end
  end
end

代码运行得到的效果符合我们的预期：

自然，在多维情况下运行，也是可以的，只需要产生多个方向的扰动即可，下面我们举一个组合优化的问题，（不是TSP，天天TSP都腻了）考虑一所学校40个新生宿舍分配的问题，调查取得了40位新生的兴趣爱好，分为“运动，音乐，游戏，书画，美食，其他”，我们希望找出一种方案，使得4个人一宿舍后，不同寝室间同寝室的两两同学的共同爱好数量分布尽可能的均匀。自然考虑“其他”这个爱好过于宽泛，这里我们就对其不作考虑了。

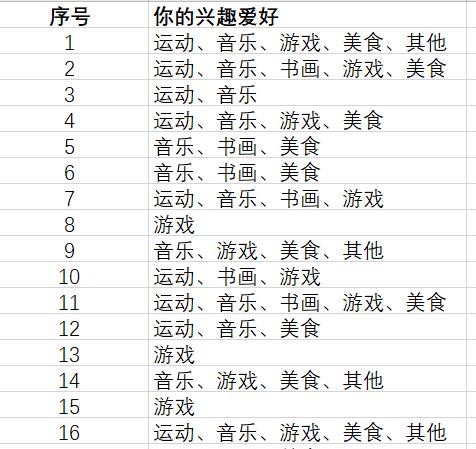
这个问题显然不能用暴力搜索来解决，我们考虑模拟退火。我们将每个同学的喜好看成一个五元组，只考虑前五个，处理excel中的数据得到五元组的0-1矩阵$A$,我们考虑$AA^T$的上三角部分，就是我们想要的同学之间共同喜好的个数.但实际上我们为了编程的方便不需要对$AA^T$作多余的处理。

为了让同寝室两两同学的爱好分布尽量均匀，我们想优化的是所有寝室的共同爱好数量的方差，我们希望它最小。

但这里好像有一个小问题，与处理函数极值问题时的随机扰动时的极值而言，这种组合类问题的“随机扰动”感觉没那么直白。根据前人对于模拟退火在TSP问题上的总结，可以有三种方法：

①交换法：将序列中的两个数交换。

②移位法：将序列中的一个片段移动到片段外的某点附近（左或右）。

③倒置法：确定两个坐标，将序列在这两个坐标间的元素逆序。

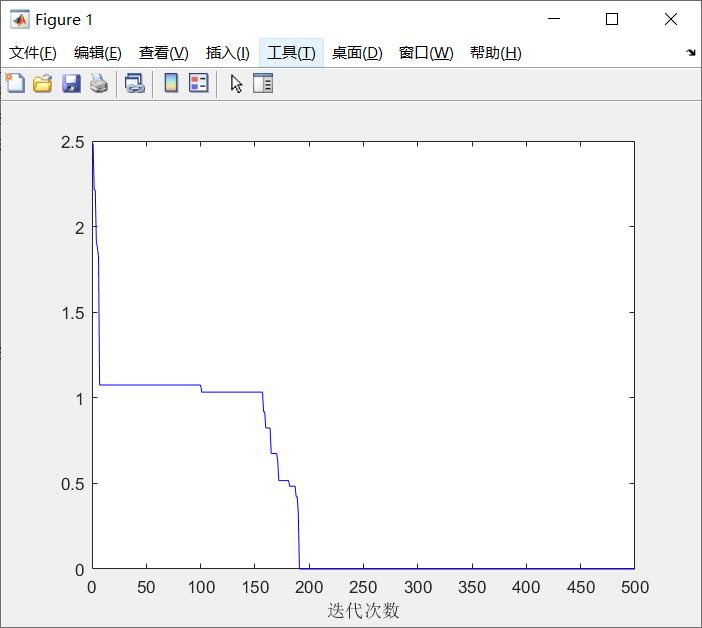
编程求解后得到最优解的迭代情况：

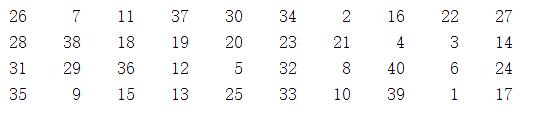
此时确实有最优方案使得方差为0：

实际上，模拟退火算法要控制的一般都是初始温度，停止温度，温度衰减系数。当然也有不同的表达方法，比如最大迭代次数等等。这个与遗传算法，粒子群算法这样的群算法不同，相对简单，应用起来也比较方便。

其实这个算法更重要的地方在于，它与玻尔兹曼机和逻辑斯蒂函数都有密切关联，前人据此构造了一种对称连接的网络，可以认为是一个无向有权全连接图，这里面单个节点$i$的能量定义为：

$E_i=\sum_j{w_{ij}s_j}+b_i$

所以整个网络的能量定义为：（负号的原因是因为我们下一步考虑的是节点从0变1的情况而概率关系中的变化量与我们习惯的末减初是反的）

$E=-\left( \sum_i{\sum_{j,i\ne j}{w_{ij}s_is_j}}+\sum_i{b_is_i} \right)$

而我们在这里注意其中单个节点$i$从0变为1造成的网络能量变化：

$\varDelta E_i=\sum_{i\ne j}{w_{ij}s_j}+b_i$

再注意最前面关于两个不同状态的概率之比的论述：

$\frac{p_{on}}{p_{off}}=\exp \left( \frac{E_{off}-E_{on}}{kT} \right)$

代入后取对数进行计算，且注意到$p_{on}+p_{off}=1$，可以推出：

$p_{on}=\frac{1}{1+\exp \left( -\frac{\varDelta E_i}{T} \right)}$

这就是著名的逻辑斯蒂函数，这个式子实际上就给出节点$i$状态为1的概率，在其他一些领域我们也能见到逻辑斯蒂函数，通过上面的分析可以得出它其中一个功用，在机器学习中我们常常会构造代价函数来使其最小化。我们一般都会比较它们的某一种范数之差，但是如果我们把这里的代价函数看作系统状态的能量，那么它应该服从玻尔兹曼分布，也就是系统获得观察数据$X$的概率可用逻辑斯蒂函数作估计。

所以有些时候会有作者直接将代价函数写成自然对数的指数，再最大化求参数，根据的就是上式。两者通过的纽带就是玻尔兹曼分布。