启发式算法

阅读数: 次 2021-08-05

有一些神棍算法在面对解空间庞大的算一天一夜都搜不出来的时候是很有效的，起码可以让我能给出一个答案，所以还是有必要整理的。

现在我们考虑眼虫藻（一种神奇的有鞭毛的可以光合作用的单细胞藻类）在一个河床中寻找阳光最充裕，也就是最高点的这么一个过程。那么会有如下的三种策略：

一只眼虫藻判断周围的亮度，一直贪婪地沿着亮度增加的方向前进，直到发现自己所在的地方相对周围而言都是最亮的，这种方法被称为爬山算法，很容易陷入局部最优。

一只眼虫藻最初佛系的随机移动，它可能走到更暗的地方，或者更亮的地方，或者亮度不变的地方。但是渐渐地它顿悟了，开始朝着最高的方向移动。这种方法称为模拟退火算法，它有可能可以跳出局部最优。

现在有一群眼虫藻，它们分别处在不同的亮度的地方生活，但是逐渐由于相对低处的有毒物质积累而渐渐杀死了在低亮度区域的眼虫藻，在较高区域的眼虫藻繁殖变异，而有毒物质也越来越向高处蔓延，最后筛选出的眼虫藻就是在最高处的眼虫藻。这种方法就是遗传算法。

这三种都是经典的启发式算法，下面来进行细致的介绍。

遗传算法

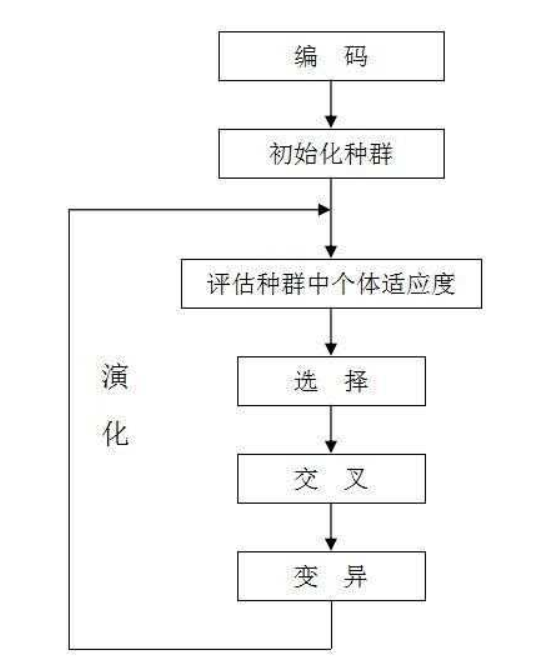
上图表示了遗传算法的流程，实际上就是：“以一种“合理”的方式优化随机出的序列”下面来举一个实际的例子来更好的体会这个过程，这里我们选取一个三角函数的最大值问题，因为它能很好的模拟我们有些问题中，极值点很多的情况。

$f(x)=9sin(5x)+8cos(4x)，x\in \left[ 0,15 \right]$

这样一个一元函数的最大值，假设我们其实画不出来这个函数的图像更不用说利用导数工具之类的。这里直接给出我写好的代码，然后一步步进行分析。

clear all
clc
popsize=30;%群体大小
chromlength=10;%字符串/染色体长度(个体长度)
pc=0.7;%交叉概率
pm=0.005;%变异概率
pop=initpop(popsize,chromlength);%初始化种群
%开始迭代
X=0:0.01:15;
Y=9.*sin(5.*X)+8.*cos(4.*X);
plot(X,Y)
for i=1:100
    [objvalue]=calobjvalue(pop);%计算当前种群相对要求解的问题的各自的值
    fitvalue=calfitvalue(objvalue);%通过上一步计算的值来得出适应度
    [newpop]=selection(pop,fitvalue);%通过适应度来进行选择，淘汰部分种群
    [newpop2]=crossover(newpop,pc);%进行交叉操作
    [newpop3]=mutation(newpop2,pm);%再进行变异操作
    y=objvalue;
    x=decodechrom(pop,1,chromlength)*15/1023;
    plot(X,Y);
    hold on
    scatter(x,y);
    action(i)=getframe;
    hold off
    %%%
    pop=newpop3;%将经过交叉变异筛选后的种群用来下一步迭代
end
%hold off
xlabel('done')
y_final=max(y)

我们知道一个染色体有一条DNA，DNA有两条链…AGCT等等，该算法吸取了这样的思想并进行了简化，意思是用一些手段将我们解空间中的值变成一串编码，这样的话对这个编码进行交叉，变异，淘汰等等操作，来模拟这个过程（是不是相当神棍？确实很神棍！）。那么对于这个具体的例子，我们怎么办呢？由于$x\in \left[ 0,15 \right] $,我们选取一个合适的染色体长度，并先用二进制编码来举例子。为了简单起见，因为我们精度不需要那么高，就确定是10了，这样的话它大概能满足小数点后三位，我们建立二进制编码与$x$的转化关系：

$\left( a_0a_1...a_{l-1} \right) _2=\left( \sum_{i=0}^{l-1}{b_i2^i} \right) _{10}=x^t \\ x=a+x^t\frac{\left( b-a \right)}{2^l-1}$

在这里，$a=0,b=15,l=10$，注意：这里编码方式是不唯一的，根据问题的不同，其实选择不同的编码方式更加合理，比如对于TSP问题，编码选择排列，自然就很科学。总之确定了这个以后我们初始化种群：

function pop = initpop(popsize,chromlength)
pop=round(rand(popsize,chromlength));
%rand均匀产生(0,1)的随机数，然后再round取整，我们最终得到以popsize为行数，chromlength为列数的矩阵
end

于是我们的pop矩阵中，一行对应着一个$x$,列数仅仅表示该条染色体的长度。

之后我们来计算此时种群对应的值：

function [objvalue]=calobjvalue(pop)
temp1=decodechrom(pop,1,10);%这里按照样例的要求,取spoint=1,length=10
x=temp1*15/1023;%将二值域的数转化为变量域的数
objvalue=9*sin(5*x)+8*cos(4*x);
end

这里decodechrom的实现因人而异，我这里分为了两个.m文件，只要可以实现就可。

%spoint是待解码的二进制串的起始位置，length表示截取的长度
function pop2=decodechrom(pop,spoint,length)
pop1=pop(:,spoint:spoint+length-1);
pop2=decodebinary(pop1);
end
%将二进制转为十进制的函数
function pop2=decodebinary(pop)
[px,py]=size(pop);%得到初始化后种群的行数px和列数py
for i=1:py
    pop1(:,i)=2.^(py-i).*pop(:,i);
end
pop2=sum(pop1,2);%sum(A,2)是对A按行求和，sum(A,1)是对A按列求和
end

然后我们用objvalue来计算适应度fitvalue,这里就牵扯到一个问题，适应度函数怎么选择比较合适：我们希望适应度函数足够简单来进行筛选，并且这个适应度函数与后面筛选的方式有关，而这一块，往往也是在不同问题中需要着重考虑的一块，对于这个问题我们如此选取：

function fitvalue=calfitvalue(objvalue)
global Con;
Con=0;
[px,py]=size(objvalue);
for i=1:px
    if objvalue(i)+Con>0
        temp=Con+objvalue(i);
    else
        temp=0.0;
    end
    fitvalue(i)=temp;
    %fitvalue(i)=objvalue(i);
end
fitvalue=fitvalue';

这里说的是，由于我们知道$f(x)$的最大值一定是个正数，所以我们令每个个体所对应的适应度形成一个类似于$ReLU$的函数，这里$Con$是用来表征筛选难度的，如果$Con$比较小，那么对种群起到的筛选作用越厉害，很可能导致种群第一轮就所剩无几；如果$Con$比较大，那么对于这个问题，就将是起不到什么筛选作用，这里的筛选实际上与下一步的轮盘赌选择法密切相关：

function [newpop]=selection(pop,fitvalue)
totalfit=sum(fitvalue);
fitvalue=fitvalue/totalfit;
fitvalue=cumsum(fitvalue); %cumsum是累积求和函数，例如fitvalue=[1 2 3 4],则cumsum(fitvalue)=[1 3 6 10]
[px,py]=size(pop);
ms=sort(rand(px,1));
fitin=1;
newin=1;
%轮盘赌选择算法
while newin<=px
    if (ms(newin))<fitvalue(fitin) || fitvalue(fitin)==max(fitvalue)
        newpop(newin,:)=pop(fitin,:);%%%%%
        newin=newin+1;
    else
        fitin=fitin+1;
    end
end

轮盘赌选择法实现的是，对于经归一化处理到0~1的适应度，适应度越高的，越有可能活下来，也就是被收入newpop的一员，但在这里根据问题的不同，我们可能会考虑无条件保留当前种群中最优的那个个体，这样可以避免它的丢失，但可能会让算法跳不出局部最优。

到这里，还算是合理，但接下来的交叉和变异操作，我是真的觉得神棍，即使它有一定的道理，上面我们定义的两个参数pc,pm就是来判定是否发生交叉和变异的参数，交叉函数的意思是，对每个个体进行一次随机数生成，当他们对应的随机数比pc小，就进行“交叉”，交叉是将两组编码真的进行“交叉互换”，这里实际上交叉函数怎么交叉，也是不一定的，对于不同的问题，可能别的交叉方法更加合适，但他们的目的都是想从已有的解里产生一些新解，而理论依据居然是：“适应度强的DNA的交叉应该会产生更强的子代”；变异的方法是类似的，当生成的随机数小于pm时进行变异，让某个位点的编码从0变1或从1变0，这也不是一定的，你可以选择不同的变异方法，我仅实现了两种最简单的。

%交叉
function [newpop]=crossover(pop,pc)
[px,py]=size(pop);
newpop=ones(size(pop));
for i=1:2:px-1
    if(rand<pc)
        cpoint=round(rand*py);
        newpop(i,:)=[pop(i,1:cpoint),pop(i+1,cpoint+1:py)];
        newpop(i+1,:)=[pop(i+1,1:cpoint),pop(i,cpoint+1:py)];
    else
        newpop(i,:)=pop(i,:);
        newpop(i+1,:)=pop(i+1,:);
    end
end
%变异
function [newpop]=mutation(pop,pm)
[px,py]=size(pop);
newpop=ones(size(pop));
for i=1:px
    if(rand<pm)
        mpoint=round(rand*py);
        if mpoint<=0
            mpoint=1;
        end
        newpop(i,:)=pop(i,:);
        for j=1:mpoint
            if newpop(i,j)==0
                newpop(i,j)=1;
            else
                newpop(i,j)=0;
            end
        end
    else
        newpop(i,:)=pop(i,:);
    end
end

接下来就是迭代求解了，之后将结果给出，在这个流程中，我们可以知道，遗传算法是要根据具体问题调整的，并且其中①染色体长度②适应度函数③相关参数（pc,pm,Con等）都要根据具体问题来进行修改，上面的例子运行后的结果是：

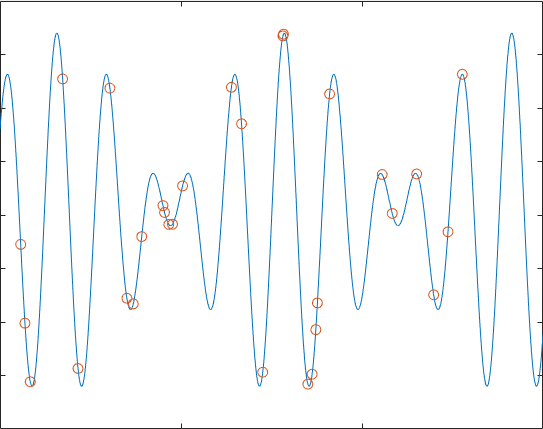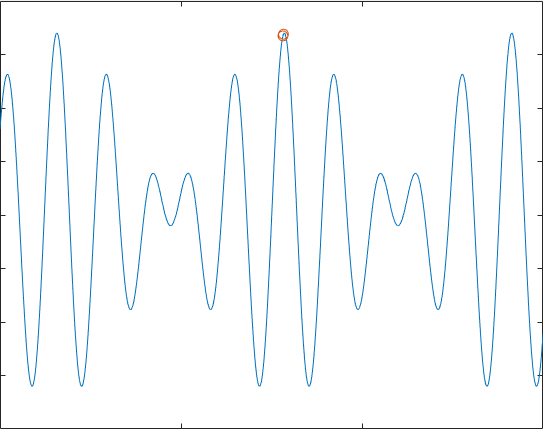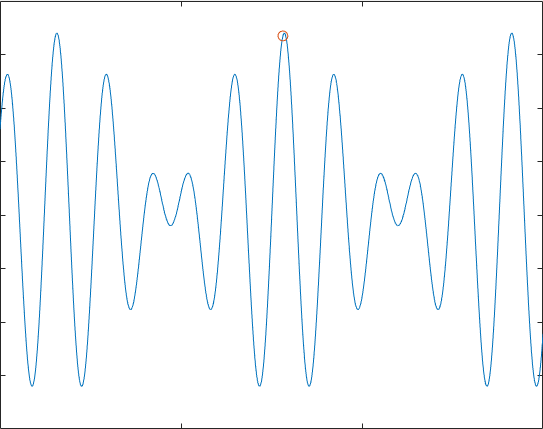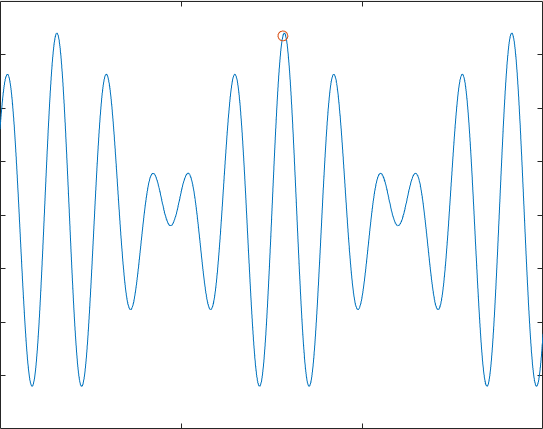
这个效果并不是特别好，我们都发现，如果多次实验，它不一定能到达最优解，有时甚至会只是停留在一个可以“可以接受的解”，但这就是有用的地方，考虑38个坐标的TSP问题，如果用蒙特卡罗模拟100000000次，得到结果为1.6843e+04,编写遗传算法实现，可以在很短的时间得到7.681e+03的效果不错的解：

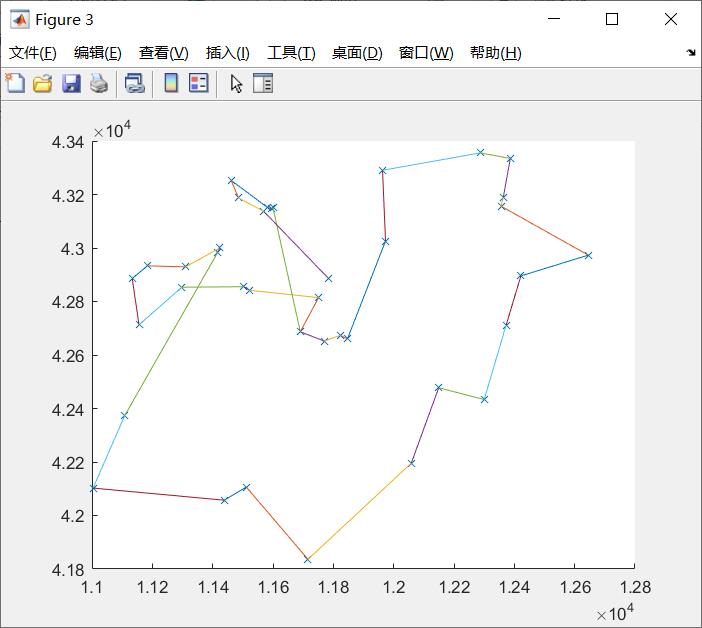
（根据公测，最短路径是6500左右），也就是说，我们即使知道它不是最优解，但是也可以将这个解拿来使用，以那个三角函数最值问题为例，假设真正的函数比这个三角函数复杂的多的多，那么用这种方法可以有效的避免高维搜索，并且得到合适的解。

但是在最后还有个比较头疼的问题，假设我在参加数学建模，拿到这个问题的时候我只有三天时间，三天时间就算仿照各种实例重建一个对应要求解的问题的遗传算法，是有难度的，并且我也不能确定结果的好坏，这里matlab给出了一个解决方案：ga()函数，它可以帮助我们用遗传算法确定最小值，调用格式：

1	x=ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon,IntCon,options)

这里fun是适应度函数句柄，nvars是x中的自变量个数，A,b是$Ax\leqslant b$的线性约束，Aeq,beq是$Aeqx=beq$的等式约束，lb,ub是自变量的下限和上限，nonlcon是非线性规划条件,IntCon是整数规划条件，options是关于遗传算法的设置，这里很多时候用不到这么的多参数，不需要的就[]或者略掉就好了。

这里面的options可以用gaoptimset(‘parameter1’,value1,’parameter2’,value2,…)的形式来调用，它的属性是，当然一般用默认的效果也很好了。

属性名	默认值	实现功能
PopInitRange	[0,1]	初始种群生成区间
PopulationSize	20	种群规模
CrossoverFraction	0.8	交叉概率
MigrationFraction	0.2	变异概率
Generations	100	超过该代数停止
TimeLimit	Inf	超过时间限制时停止
FitnessLimit	-Inf	最佳个体等于或小于适应度
InitialPopulation	[]	可以用上次遗传生成的种群作为下一次的初始值
EliteCount	0	用于精英原则，每次一定活下来的个体数

应用封装好的的ga()函数，解决之前的问题只需

ObjectiveFunction = @simple_fitness;
nvars = 1;%变量个数
LB = [0]%定义域下限
UB = [15]%定义域上限
 
[x,fval] = ga(ObjectiveFunction,nvars,[],[],[],[],LB,UB)%调用ga函数


function y = simple_fitness(x)
 
y = 9*sin(5*x)+8*cos(4*x);
y=-y;%%求的是最大值，要变号
 
end

至此就有了一个相对圆满的应对短时间内的解空间巨大的优化问题的解决方案，虽然它的优化依据十分玄学，但能抓到耗子的都是好猫orz。