事情是因为我看了一篇关于故障诊断(fault diagnosis)的综述,我看完了大受震撼,于是进行了一部分整理,那里面的相当多的内容对我来说还是太难了qwq。
查阅资料发现,故障诊断可分为定性和定量两类,随着现在对精细化的进一步要求,定量应该会称为主流,而这篇综述正全是关于定量的,该综述的骨架是:
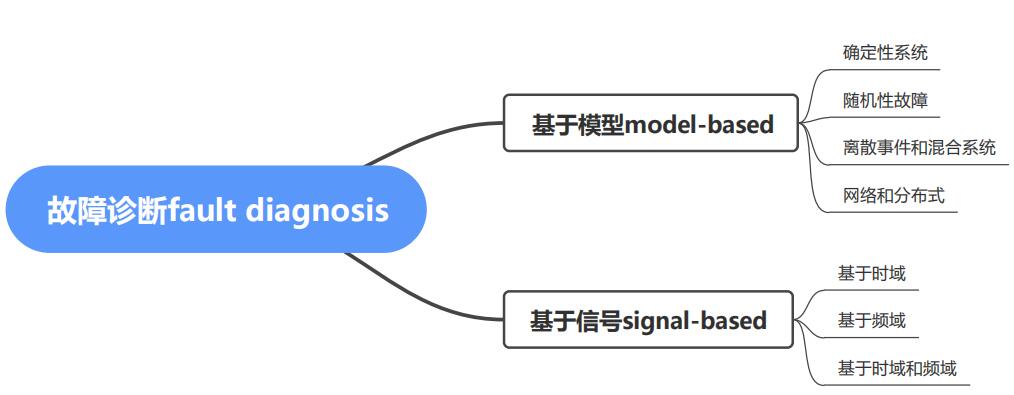
虽然上面这张图很简单,但是具体内容还是相当多的。
introduction
文章的第一部分讲述了故障诊断中一些的一些概念,故障分为三种:驱动器故障(actuator faults),传感器故障(sensor faults),设备故障(plant faults)。第一个是指例如马达的堵塞,第二个是指例如一些关键的传感器只卡在一个指,第三个是指例如某些模块断连。这些故障一般会导致控制器控制作用的中断,这样会产生大量误差,或者直接改变系统的输入输出特性,导致系统性能下降甚至是损坏。
人们经常用冗余(redundancy)这个概念来进行故障诊断,分为硬件冗余和软件(分析性)冗余:
硬件冗余说的是,对于一个系统,我们只需要再备份一个和其完全一致的系统,通过给定相同的输入侦测变化,就能找到问题。这个办法很有效,但是成本很高。因为这种方法很多时候都需要有充足的关键部分的冗余副本。并且结合一些流水线上的实际,安装也是一个困难。
软件(分析性)冗余是依据现代控制理论的成熟而产生的一种故障诊断的方法。他是基于我们对正确数据的前有经验,来设计一套特定的算法来进行故障诊断的推理。
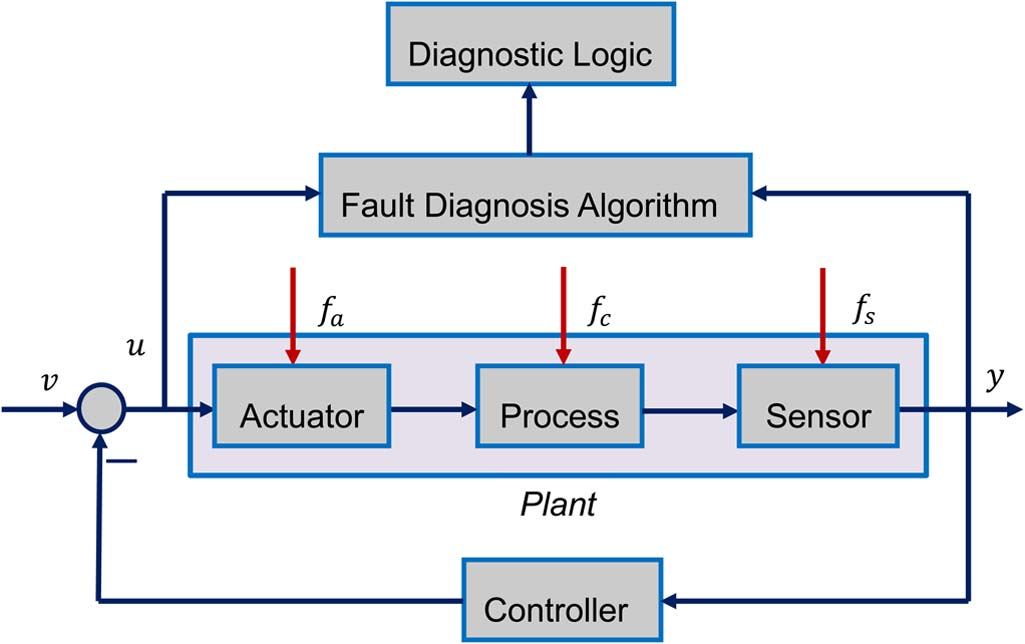
其中$f_a,f_c,f_s$分别是对这各自的故障影响,其中的输入量$u$和输出量$y$反馈给故障诊断算法来进行推理。
故障诊断有三个任务,首先是确定故障发生的时间,再确定故障的位置,最后确定故障的细节(大小,类型,形状,等等),最终得到这些结果以后,期望容错系统响应来作用到控制器上以纠正错误。
文章作者在引言部分的最后给出了近年来在上面那些方面的一些实践成果(#TODO)
Model-Based fault diagnosis methods
如果我们能知道所要进行故障检测的系统的全部机理,那么建立一个普适的模型运用机理方法来监测实际和理论的一致性,就能很好的起到故障检测的作用。这只是个宽泛的理念,在不同系统中所涉及的内容是很多的。
Deterministic fault diagnosis
为了简单起见,我们假设一个线性定常系统:
这里$x(k)$表征系统此时的状态,$u(k)$表示此时给定的输入,$y(k$)表示测量得到的输出,$f_a,f_c,f_s$与前面的意义一致,$d(k)$表示系统本身的自反馈的干扰,$\omega(k)$表示环境噪声。带$\varDelta$的大写字母表示由于我们测量出的模型与真实的差距(误差)
那么一个故障诊断的滤波器(我不是很清楚为什么要这么叫)就可以是,但它的意义确实很容易理解:
这样给出的是$x,y$的估计值和残差$r$。我们综合上面两个方程组,可以看出,残差$r$不仅和我们前面说的$f_a,f_c,f_s$有关,还与$d,\omega$有关,即残余信号受到了故障信号和干扰信号的共同影响,文章指出,残余信号经推导可以写作:
这里$G,f$的具体计算方法见文章,我们只需知道,我们期望残余信号中,干扰信号的影响小一些,而故障信号的影响能大一些,这样的话计算的$r$就能更加准确,所以在实际问题中这就会变成一个最优化问题:我们期望表征干扰信号矩阵的范数与表征故障信号矩阵的范数的比值最小
综述作者进一步给了许多文献来给出在这一方面的成果:即最优参数$K$的选取经研究可以变为寻找最优特征值和特征向量等等,这里还涉及了LMI线性矩阵不等式这一工具(#TODO)
stochastic fault diagnosis
该小节介绍的是一种结合随机方法的故障检测,它主要强调了对得到的数据进行的概率论与数理统计方向的知识,其中频繁提到了卡尔曼滤波器
(为什么都管他们叫“滤波xxx”)
卡尔曼滤波说的是通过系统的输入输出观测数据,对系统状态进行最优估计,由于其中已经包含了系统中噪声和干扰的影响,所以最优估计也看作是一种滤波过程。我找到了一个很实用的例子来帮助我理解这个方法:
假设想知道一个房间的温度,我们根据体感温度来判断,经验上认为温度是恒定的,但是我们对我们的经验并不能100%相信,可能存在一些偏差,我们将这个偏差看作是噪声,同时我们在房间里也安放一个温度计,温度计也不是100%准确,测量值和真实值存在偏差,现在我们要根据我们的经验温度和温度计的测量值以及他们各自的偏差来估算这个房间的实际温度,那么如何估算最优呢?
那么如果说要估算$k$时的实际温度值,首先要根据$k-1$时的温度值来预测$k$时的经验温度,假设为23度,由于我们相信温度是恒定的,那么$T_k=T_{k-1}$,同时此时经验温度的偏差是5度(5度这样计算,$k-1$时估算的最优温度偏差是3,对自己预测的不确定度是4,那么$\sqrt{3^2+4^2}=5$),之后又从温度计那里得到了$k$时刻的温度值,假设是25度,同时该值的偏差是4度。
现在的问题就是,为了估算实际的温度,我们到底是相信自己的23度多一点,还是相信温度计的25度多一点,也就是说我们想要一个权重,来计算
由中心极限定理,经验温度和测量温度实际都从属于温度$T$的正态分布,那么他们分布的均值是相同的,而他们分布的标准差可以写作:$\sigma _a,\sigma _b,\sigma _c$,由概率论的知识,$\sigma _c=\sqrt{k^2\sigma _{a}^{2}+\left( 1-k \right) ^2\sigma _{b}^{2}}$,我们希望这个值越小越好,那么就应该取其中的$k=\sigma _{b}^{2}/\left( \sigma _{a}^{2}+\sigma _{b}^{2} \right) $,这是一个二次函数的极值条件,那么在我们的例子里:$k=\frac{5^2}{5^2+4^2}$,这里由于某些神秘的原因(等我把贝叶斯学明白了就回来填坑),这个权重实际上是$\sqrt k=0.78$,之后我们将其代入,求得最优的$T$,同时这个$T$也称为计算$k+1$时的依据,就是这样的一个“动态回归”的过程:
这是一般形式的卡尔曼滤波,把它写在这里的作用主要是提醒我要打好数理基础orz以及记得去学概率论与数理统计。
(这个玩意用在小车里估计挺好的,它迭代速度快而且不怎么占空间)
for Discrete-Events and Hybrid Systems
这里主要指的是对于一些动态变化的离散系统,以及一些复杂的工业系统,一方面他们既有基于时间的连续动力学模型,又有事件驱动的离散动力学模型,哎我怎么在哪里看见过这个。
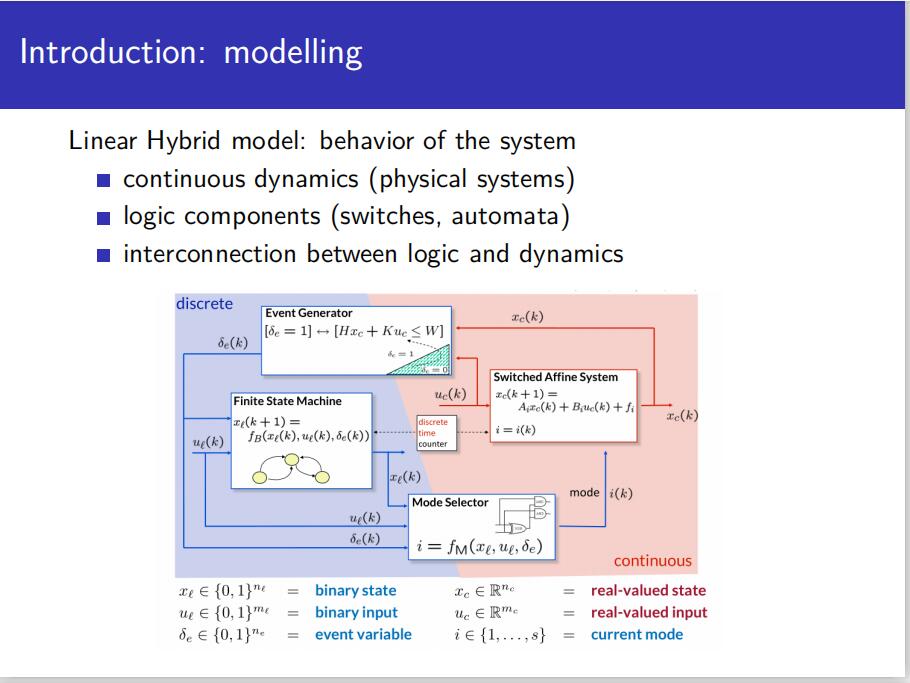
这块由于太与具体示例结合了,挺麻的,“不具有普适性”。
for Networked and Distributed Systems
这一段…给的文献综述,我没有什么网络的前置知识属实是读不懂,先鸽掉了。
Signal-Based fault diagnosis method
由于实际中的某些系统可能机理过于复杂等原因,这一块提出的是基于信号的故障检测的方法,也就是说我们不依托这个系统本身的机理,仅仅从它的信号特征上,由已有的先前的经验进行故障检测。
Time-Domain
时域方法是指分析信号的时域特征,例如峰值,均值,均方根,方差以及据此定义的一系列指标,在这里文中提到了一些很有用的算法: fast dynamic time warping(fast DTW),correlated kurtosis(CK), scale-invariant feature transform(SIFT)…
Frequency-Domain
频域方法是说利用频谱分析工具来进行检测变化和故障,例如离散傅里叶变换,这里特别地提及了一种诊断电机故障的电机电流特征分析法(MCSA),考虑到这个以后可能要用到,我对其进行了一下查阅,找到了一个用MCSA法测量异步电机转速的方法,来简单了解一下这种方法。
它的原理说的是电机运转时由于结构组成,转子电流感应产生一个有效的转子磁场,会在定子绕组中感应产生很小的电流,并形成一个高次谐波旋转磁场,因此转子频率可以通过检测定子电流频谱得到:
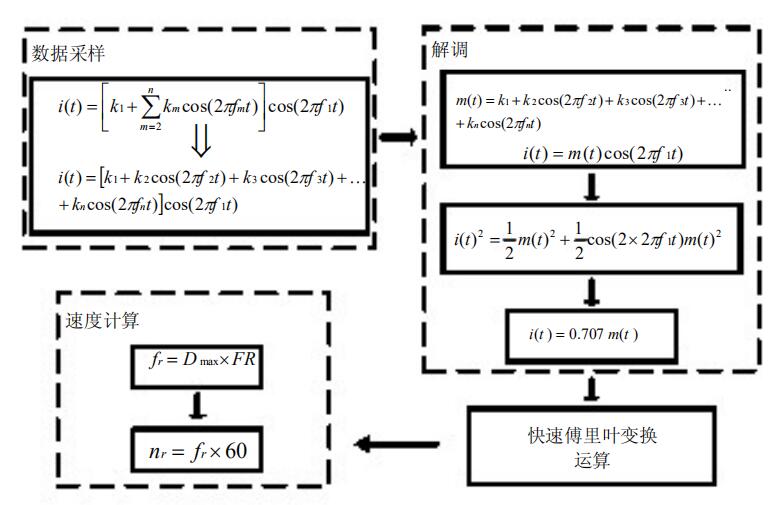
据我推测,这个技术的核心应该还是傅里叶变换,并且如果它只计算电机转速的话,那么得到的频率的大小实际上就是无关紧要的,也就是说这个技术应该不仅可以测转速。
Time-Frequency
这个方法结合了时域和频域,因为考虑到纯时域或者纯频域的方法进行检测,可能对某些瞬时变化的信号来说会有困难,于是人们用了很多时频分析方法:
短时傅里叶变换(STFT),小波变换(WT),Hibert-Huang变换(HIT),Wigner-Ville分布(WVD)等等……
我试图了解一下这些方法,但是,我连他们的基础—傅里叶变换的本体还没有看明白……

