偏微分方程3

阅读数: 次 2021-08-01

由于偏微分方程数值方法和计算其解析解是一块非常庞大的内容，并且我以及队友的专业都不是数学/物理方向，但其中已经涉及了相当一部分数值分析和数学物理方法的内容，考虑到以上原因本文只局限在数学建模中够用的且很肤浅的范围内总结一些内容。

不同的差分格式

实际上差分格式大多大同小异，不同差分格式的稳定性和精度都有所不同，针对具体问题应该选择合适的差分格式，下面主要介绍三种比较重要的格式：

最简隐格式

我们以一维热传导时的情况举例，如果是最简隐格式，实际上就是：

$\frac{u_{j}^{n+1}-u_{j}^{n}}{\tau}=\frac{u_{j+1}^{n+1}-2u_{j}^{n+1}+u_{j-1}^{n+1}}{h^2}$

注意到右边，右边的时间状态是$n+1$,那就注意到一个问题了，既然是迭代求解的，在尚未知道$n+1$时的状态时，这个等式是如何进行迭代呢？这实际上就是隐格式的特点，需要借用一些代数方程组再来联立，在最简隐格式中，常用的是用最简显格式先得到一个迭代初值，然后代入上面再反复迭代，直到结果稳定（收敛）后，所以，最简隐格式是无条件收敛的（这点在后面再详细论述），但它比较耗时。

Crank-Nicolson格式

$\frac{u_{j}^{n+1}-u_{j}^{n}}{\tau}=\frac{a}{2}\left[ \frac{u_{j+1}^{n+1}-2u_{j}^{n+1}+u_{j-1}^{n+1}}{h^2}+\frac{u_{j+1}^{n}-2u_{j}^{n}+u_{j-1}^{n}}{h^2} \right]$

观察可知，这种方法其实也是一种隐式方法，实际上是向前差分格式和向后差分格式作算数平均，这种格式使用起来比较方便，我们记$\beta =\frac{a\tau}{2h^2}$,再对上面的式子进行移项处理，对于整理后的形式，我们发现它可以写成：

$\left( \beta ,-1-2\beta ,\beta \right) \left( \begin{array}{c} u_{i-1}^{j+1}\\ u_{i}^{j+1}\\ u_{i+1}^{j+1}\\ \end{array} \right) =\left( -\beta ,2\beta -1,-\beta \right) \left( \begin{array}{c} u_{i-1}^{j}\\ u_{i}^{j}\\ u_{i+1}^{j}\\ \end{array} \right)$

也就是说可以写为这样的矩阵形式：$AU^{n+1}=BU^n$,左乘$A^{-1}$就能得到我们需要的计算方式。

紧致差分格式

实际上我们作离散化时都是用特定的一些节点来逼近想要的对象，紧致差分格式说的是利用函数值的某种线性组合，来表示我们所需的导数值，其实原理非常的简单。

对于一阶导数的紧致差分格式，目标上是想得到：

$\beta f_{i-2}^{'}+\alpha f_{i-1}^{'}+f_{i}^{'}+\alpha f_{i+1}^{'}+\beta f_{i+2}^{'}\\=c\frac{f_{i+3}-f_{i-3}}{6h}+b\frac{f_{i+2}-f_{i-2}}{4h}+a\frac{f_{i+1}-f_{i-1}}{2h}$

这里参数的确定直接应用$Taylor$级数展开，用待定系数法即得

$\begin{array}{c} a+b+c=1+2\alpha +2\beta\\ a+4b+9c=6\alpha +24\beta\\ a+16b+81c=10\alpha +160\beta\\ \end{array}$

当满足第一个式子时，可以得到具有二阶精度的差分格式，同时满足第一个和第二个式子时候，可以得到具有四阶精度的差分格式，如果三个式子都满足，可以得到具有六阶精度的差分格式。

我们根据需要选取合适的取值，即可得到所需的差分格式，例如：

$\frac{1}{4}f_{i-1}^{'}+f_{i}^{'}+\frac{1}{4}f_{i+1}^{'}=\frac{3}{4h}\left( f_{i+1}-f_{i-1} \right)$

就是一个具有四阶精度的紧致差分格式。

对于二阶导数的紧致差分格式，道理是一样的，目的是指得到：

$\beta f_{i-2}^{''}+\alpha f_{i-1}^{''}+f_{i}^{''}+\alpha f_{i+1}^{''}+\beta f_{i+2}^{''}\\=c\frac{f_{i+3}-2f_i+f_{i-3}}{9h^2}+b\frac{f_{i+2}-2f_i+f_{i-2}}{4h^2}+a\frac{f_{i+1}-2f_i+f_{i-1}}{h^2}$

也是进行$Taylor$级数展开，最后选取合适的参数值，例如：

$\frac{1}{10}f_{i-1}^{''}+f_{i}^{''}+\frac{1}{10}f_{i+1}^{''}=\frac{6}{5}\left( \frac{f_{i+1}-2f_i+f_{i-1}}{h^2} \right)$

就是一种四阶精度的紧致差分格式。

关于稳定性和解析解

在简单介绍这部分内容之前，要先作下面的铺垫：

我们知道，对于符合傅里叶级数展开的条件的函数：

$f_T\left( t \right) =\frac{a_0}{2}+\sum_{n=1}^{\infty}{\left( a_n\cos n\omega t+b_n\sin n\omega t \right)}$

且由欧拉公式：

$e^{i\theta}=\cos \theta +i\sin \theta \\ \cos \theta =\frac{1}{2}\left( e^{i\theta}+e^{-i\theta} \right) \\ \sin \theta =-\frac{i}{2}\left( e^{i\theta}-e^{-i\theta} \right)$

我们将两者联立，可以得到：

$f_T\left( t \right) =c_0+\sum_{n=1}^{\infty}{\left( c_ne^{in\omega t}+c_{-n}e^{-in\omega t} \right)} =\sum_{-\infty}^{\infty}{c_ne^{in\omega t}}$

之后如果我们求解$c_n$的表达式，会发现：$c_n=\frac{1}{T}\int_{-T/2}^{T/2}{f_T\left( t \right) e^{-in\omega x}\mathrm{d}t}$,此时居然表达式是不需要额外讨论而完全一致的，从而：

$f_T\left( t \right) =\sum_{-\infty}^{\infty}{c_ne^{in\omega t}}$

就是傅里叶级数的复数形式，现在我们有了两种傅里叶级数的表达，在这里我们将$\omega =\frac{2\pi}{T}$称为基频率，因为它是由该函数的周期而唯一确定的。现在我们来直观感受一下这两种表达方式的区别：

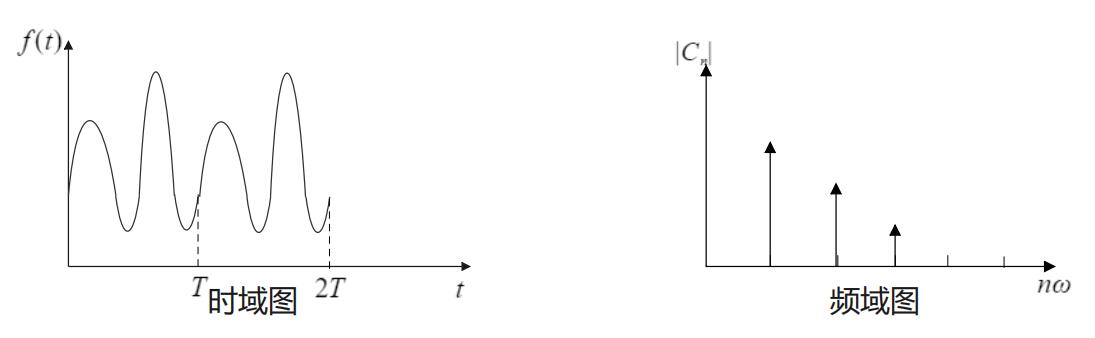
其中时域图是我们很熟悉的，而频域图则有些陌生，实际上，我们考虑傅里叶级数的每一项，$c_n$是一个函数，不同的$n$对应着不同的$c_n$。我们取它的模长，按照$n\omega$来作为横轴，而不同$n$时与$e^{inwt}$的线性组合，即是傅里叶级数。换句话说，就类似千手观音，如果我们掌握着构成某个函数的傅里叶级数，那么他们就在这个函数背后按照一排站好，侧过去看，实际上就是频域图。

但直到这里，好像还和我们要研究的内容没有什么关系，因为我们直觉上就知道大多数偏微分方程的解它肯定不是周期函数，所以我们还要把上面的内容再延申一下。

对于非周期函数，即考虑周期趋近于无穷的时候，那么我们说的基频率$\omega$会相当的小，频域图会从离散的分立点构成一个连续的曲线。此时上面的积分上下限也从$\frac{T}{2}$变为$\infty$，并且此时的$n\omega$会越来越接近为我们熟悉的“自变量$\omega$”，此时频域图中分立点的间隔$\varDelta \omega %$也变得越来越小，即：

$\sum_{n=-\infty}^{+\infty}{\varDelta \omega}\rightarrow \int_{-\infty}^{+\infty}{d\omega}$

之后我们将$c_n$的表达式连同我们上一段在周期趋于无穷时的延伸，全部带入原式：

$f\left( t \right) =\frac{1}{2\pi}\int\limits_{-\infty}^{+\infty}{\left[ \int_{-\infty}^{+\infty}{f\left( t \right) e^{-i\omega t}dt} \right] e^{iwt}dw}$

这个式子，括号里，正是傅里叶变换，而将括号内看成整体$F(\omega)$，这个式子就是傅里叶变换的逆变换。它的意义非常深刻

下面我们来讨论稳定性，所谓稳定性，大多是在有时间变量的问题里所提及的，如果选择的时间步长不合适，可能会出现这样类似爆炸，使人大为震撼的情况：

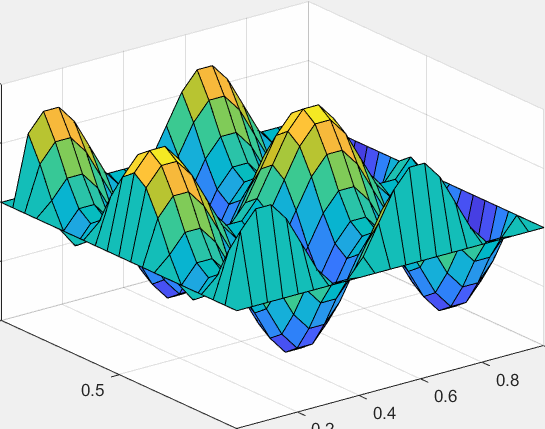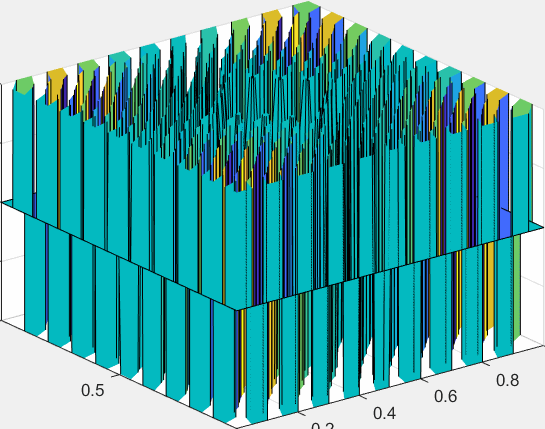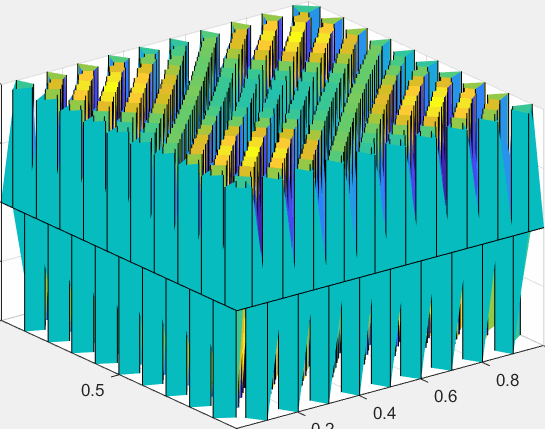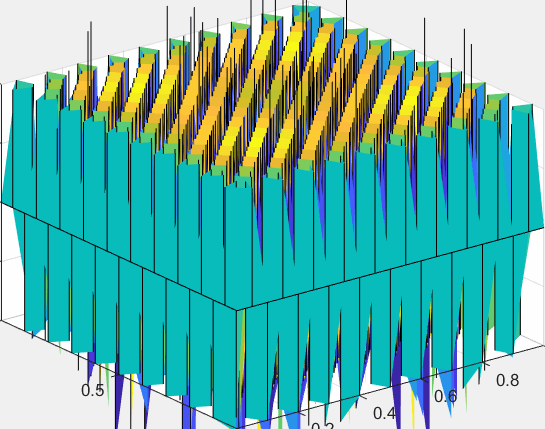
一种经典的分析差分格式稳定性的方法就是：傅里叶分析法。

这里我们只给出具有指导意义的结论：将迭代时的$U_{j}^{n}$改写成复变量$v_ne^{ijk\varDelta x}$,只要计算$G=v_{n+1}/v_n$，如果对于任意实数$k$来说$G$的模长都小于1，那么格式就是稳定的。

最后我们再说一下解析解的问题，实际上很多时候我们并不是很需要一个偏微分方程的解析解…但是有的时候，对于一些三维无界问题，找出解析解更加方便，那么上面说的傅里叶变换和解这个偏微分方程有什么关系呢？

我们考虑这样的一维波动方程：

$\frac{\partial ^2u}{\partial t^2}=\frac{\partial ^2u}{\partial x^2},-\infty <x<+\infty ,t>0$

这个方程令我们麻爪的是：它有对不同量的多次微分，这很难整。但这个问题已经被前人解决了，我们下面这样来理解这个过程，由于傅里叶变换的作用区间是负无穷到正无穷，我们记对空间变量$x$的傅里叶变换为：

$\overset{~}{U}\left( \omega ,t \right) =\int_{-\infty}^{+\infty}{u\left( x,t \right) e^{-i\omega x}dx}$

我们对方程两边也作傅里叶变换，观察一下会发生什么：

$\mathcal{F} \left[ \frac{\partial ^2u}{\partial x^2} \right] =\int_{-\infty}^{+\infty}{\frac{\partial ^2}{\partial x^2}\left( u\left( x,t \right) e^{-i\omega x} \right) dx}=\left( -i\omega \right) ^2\int_{-\infty}^{+\infty}{u\left( x,t \right) e^{-i\omega x}dx}=-\omega ^2\overset{~}{U}\left( \omega ,t \right) \\\mathcal{F} \left[ \frac{\partial ^2u}{\partial t^2} \right] =\int_{-\infty}^{+\infty}{\frac{\partial ^2}{\partial t^2}\left( u\left( x,t \right) e^{-i\omega x} \right) dx}=\frac{d^2}{dt^2}\overset{~}{U}\left( \omega ,t \right)$

实际上，傅里叶变换把多次偏微分直接“取”了出来，就像我们曾经求导不好求而取对数一样。而关于时间的偏微分化为常微分，这样当我们求得傅里叶变换后的$U(\omega,t)$后，再对它作傅里叶逆变换，就得到了之前的解。具体的计算过程这里就从略了。

实际上数学物理里还有更多的求解方法，但这里就不介绍了。

这里我举一个实际例子来说明这种办法的功用，我们假设一个扩散源在$(x_0,y_0,z_0)$且满足$Cauchy$问题的扩散问题：

$\left\{ \begin{array}{c} \frac{\partial u}{\partial t}=a^2\frac{\partial ^2u}{\partial x^2}+b^2\frac{\partial ^2u}{\partial y^2}+c^2\frac{\partial ^2u}{\partial z^2}-k^2u,\\ u\left( x,y,z,0 \right) =M\delta \left( x-x_0 \right) \delta \left( y-y_0 \right) \delta \left( z-z_0 \right)\\ \end{array} \right.$

记$\omega =\left( \omega _1,\omega _2,\omega _3 \right) $,$\overset{~}{u}\left( t,\omega \right) =\mathcal{F} \left[ u\left( x,y,z,t \right) \right] $。我们对三个空间变量以及初始条件作傅里叶变换，最后得到：

$\left\{ \begin{array}{c} \frac{d\overset{~}{u}}{dt}+\left( a^2\omega _{1}^{2}+b^2\omega _{2}^{2}+c^2\omega _{3}^{2}+k^2 \right) \overset{~}{u}=0,\\ \overset{~}{u}\left( 0,\omega \right) =Me^{-i\left( \omega _{1}^{}x_0+\omega _{2}^{}y_0+\omega _{3}^{}z_0 \right)}\\ \end{array} \right.$

（这里初始条件是$Dirac$函数的性质）

解这个常微分方程后，得到唯一解，再对齐进行傅里叶逆变换，得：

$u\left( x,y,z,t \right) =\frac{M}{\left( 2\sqrt{\pi t} \right) ^3\sqrt{a^2b^2c^2}}\exp \left\{ -\frac{\left( x-x_0 \right) ^2}{4a^2t}-\frac{\left( y-y_0 \right) ^2}{4b^2t}--\frac{\left( z-z_0 \right) ^2}{4c^2t}-k^2t \right\}$

实际上走这一套流程的时候，如果要独立的计算出来所涉及的数学知识可能有很多，所以并不是很方便，把解析解的内容写上来只是起到“知道”就行的作用，实践时还是应以数值方法为主。

应该到这里偏微分方程的内容就结束了，我希望我的队友…有在家好好学习，嗯……只是希望。

完结撒花！