偏微分方程2

阅读数: 次 2021-07-31

与微分方程一样，偏微分方程也有解析解和数值解之分，但它的解析解有时不是很方便，我们先介绍它的数值解，在后面再对一些解析解进行补充。

数值解离不开一个重要的方法：有限差分法，实际上就是将难以求解的问题离散化成计算机可以迭代求解的简单问题。下面将结合几个简单的情形来对其进行说明和实现。

有恒定热源的一维热传导情形

$\left\{ \begin{array}{c} \frac{\partial u}{\partial t}=a^2\frac{\partial ^2u}{\partial x^2}+f\left( x,t \right)\\ u\left( x,0 \right) =\varphi \left( x \right)\\ \end{array} \right.$

其中$f\left( x,t \right) $表示热源，不失一般性，我们将$x,t$的取值设为从0到$x_m,t_m$,建立二维平面网格$x\times t$

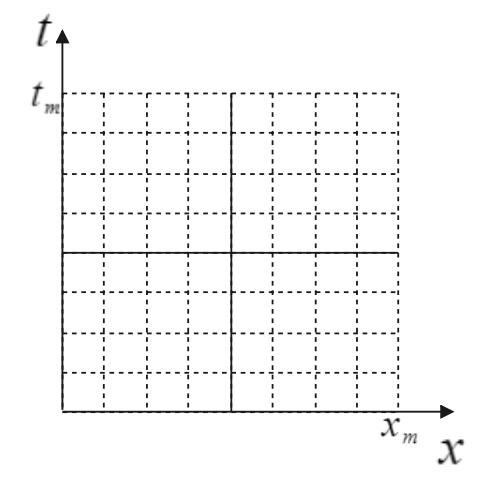
则时间步长和空间步长满足：

$\left\{ \begin{array}{c} x_j=0+\left( j-1 \right) \varDelta x\\ t_n=0+\left( n-1 \right) \varDelta t\\ \end{array} \right.$

如同在用数值方法解微分方程时的一样，我们将$u\left( x_j,t_n \right)$近似为$u_{j}^{n}$,而$f\left( x_j,t_n \right)$直接记作$f_{j}^{n}$,注意在这里热源函数是没有近似的。在这里我们约定时间的角标至于函数符号的右上角，虽然我们更加熟悉$u_{j,n}$这样的形式，但是我们为了和后面的内容一致，对此作出改变。如果不记得为什么$u$是近似而$f$不是，可以回顾一下显式欧拉法求解微分方程产生误差的过程。

接着就是选取合适的差分格式，在这里为了方便起见，我们选用最简显格式来说明，将上式离散化，不难得出：

$\frac{u_{j}^{n+1}-u_{j}^{n}}{\varDelta t}=\frac{a^2}{\varDelta x}\left( \frac{\left( u_{j+1}^{n}-u_{j}^{n} \right) -\left( u_{j}^{n}-u_{j-1}^{n} \right)}{\varDelta x} \right) +f_{j}^{n}$

我们整理离散化后的表达式，观察不难得到，将$u_{j}^{n+1}$写到方程的一侧会显得简洁不少，得到：

$u_{j}^{n+1}=\left( \frac{a^2}{\varDelta ^2x}\left( u_{j+1}^{n}-2u_{j}^{n}+u_{j-1}^{n} \right) +f_{j}^{n} \right) \varDelta t+u_{j}^{n}$

而我们为了能编程求解这个问题，往往希望它能被写作向量形式，即矩阵运算，实际上我们发现，对于上面的式子，左侧相同的$n+1$不同的$j$正可以构成一个列向量，而右侧的$u_{j+1}^{n}-2u_{j}^{n}+u_{j-1}^{n}$也可以写作：

$\left( 1,-2,1 \right) \left( \begin{array}{c} u_{j-1}^{n}\\ u_{j}^{n}\\ u_{j+1}^{n}\\ \end{array} \right)$

那么实际上对于不同的$j$,可以写成这样的迭代表达式：

$\overrightarrow{u^{n+1}}=\left( \frac{a^2}{\varDelta ^2x}A\overrightarrow{u^n}+\overrightarrow{f^n} \right) \varDelta t+\overrightarrow{u^n}$

实际上就是：

$\left( \begin{array}{c} \begin{array}{c} u_{1}^{n+1}\\ u_{2}^{n+1}\\ \end{array}\\ ...\\ u_{j_{\max}}^{n+1}\\ \end{array} \right) =\frac{a^2\varDelta t}{\varDelta ^2x}\left( \begin{matrix}{l} *& *& ..& ..& *\\ 1& -2& 1& & \\ & ..& ..& ..& \\ & & 1& -2& 1\\ *& ..& ..& *& *\\ \end{matrix} \right) \left( \begin{array}{c} \begin{array}{c} u_{1}^{n}\\ u_{2}^{n}\\ \end{array}\\ ...\\ u_{j_{\max}}^{n}\\ \end{array} \right) +\varDelta t\left( \begin{array}{c} \begin{array}{c} f_{1}^{n}\\ f_{2}^{n}\\ \end{array}\\ ...\\ f_{j_{\max}}^{n}\\ \end{array} \right) +\left( \begin{array}{c} \begin{array}{c} u_{1}^{n}\\ u_{2}^{n}\\ \end{array}\\ ...\\ u_{j_{\max}}^{n}\\ \end{array} \right)$

这里实际上$A$矩阵的第一行和最后一行取什么元素是无关紧要的，因为从表达式中我们可以看出，实际上对于$n$时的$1$到$j_{max}$，从离散化后的方程中只能得到$n+1$时$2$到$j_{max}-1$的信息，至于此时的$1$与$j_{max}$,是由边界条件决定的，但为了编程时的方便，我们可以直接用这样的matlab命令构造稀疏矩阵：

1	A=-2*eye(length(x))+diag(ones(1,length(x)-1),1)+diag(ones(1,length(x)-1),-1)

在这里，ones()先构造了一行$n-1$列的全1矩阵，之后diag()将这个全1矩阵作为向量V生成A的第k条对角线，当k=1时是主对角线上方的次对角线，k=-1时是下方的。最后再用eye()构造单位矩阵生成主对角线元素。

下面我们举一个具体的例子来进行实践，考虑如下的一元热传导方程：

$\left\{ \begin{array}{c} \frac{\partial u}{\partial t}=\frac{\partial ^2u}{\partial x^2}\,\,0<t<0.03,0<x<1\\ u\left( x,0 \right) =\sin \left( 4\pi x \right) \,\,0\leqslant x\leqslant 1\\ u\left( 0,t \right) =0, 0\leqslant t\leqslant 0.03\\ u\left( 1,t \right) =0, 0\leqslant t\leqslant 0.03\\ \end{array} \right.$

我们用上面的思路进行编程求解：

作出温度关于时间和空间演变的曲面：

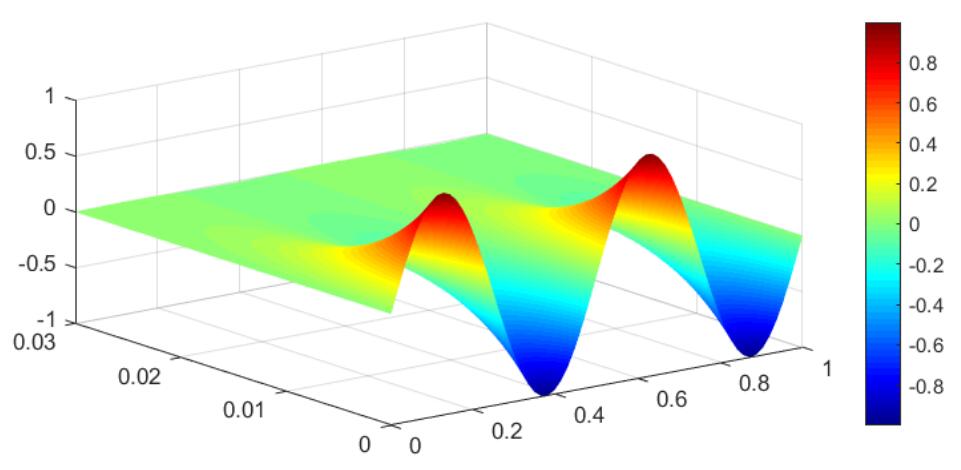
实际上上面这个问题是有解析解的：$u\left( t,x \right) =e^{-\left( 4\pi \right) ^2t}\sin \left( 4\pi x \right) $,并且我们将解析解与数值解作对比，发现数值解效果很好。实际上数值解的好坏很大程度上取决于步长的选取，在最简显格式下步长产生的误差会不断积累，至于偏微分方程的解析解如何得到，在后面会进行介绍。

有恒定热源的二维热传导情形

当维数升高时，我们处理起来的难度就有所增加，仅仅上面一维的情况就需要我们用三维来表示了，对于二维的热传导清形，我们有：

$\left\{ \begin{array}{c} \frac{\partial u}{\partial t}=a^2\left( \frac{\partial ^2u}{\partial x^2}+\frac{\partial ^2u}{\partial y^2} \right) +F\left( x,y,t \right)\\ u\left( x,y,0 \right) =\varphi \left( x,y \right)\\ \end{array} \right.$

和一维时的情形一样我们来确定步长：

$\left\{ \begin{array}{c} x_i=0+\left( i-1 \right) \varDelta x\\ y_j=0+\left( y-1 \right) \varDelta y\\ t_n=0+\left( n-1 \right) \varDelta t\\ \end{array} \right.$

此时，$u\left( x_i,y_j,t_n \right)$近似为$u_{i,j}^{n}$，我们将$n$时$(x,y)$的温度分布记为矩阵$U^n$，那么此时对于一个$n$时的温度分布就不仅是一个列向量了，而是一个矩阵，而且我们注意到，我们在一维时处理过二阶差商，当时我们取的是相同的时间，不同的$x$构成的一个列向量，而现在则是许多列的列向量组成的矩阵，而对于选取的一列，他们$y$相同而$x$不同，对其进行这样的操作是在对$x$求二阶差商。那么反过来，而如果我们想对$y$求二阶差商，只需要将行向量处理为之前的列向量，注意到$A$矩阵是对称矩阵，那么实际上$U^nA_y$就是求对$y$求二阶差商的做法。

这样我们就得到了迭代表达式：

$U^{n+1}=a^2\varDelta t\left( \frac{1}{\varDelta ^2x}A_xU^n+\frac{1}{\varDelta ^2y}U^{n}A_y+F^n \right) +U^n$

(认真观察会发现两个$A$并不相同，我们借用下面的例子在实践上作更详细的说明。)

考虑如下的二维热传导方程：

$\left\{ \begin{array}{c} \frac{\partial u}{\partial t}=\frac{\partial ^2u}{\partial x^2}+\frac{\partial ^2u}{\partial y^2},x,y\in \left[ 0,1 \right]\\ u\left( x,y,0 \right) =\sin \left( 4\pi x \right) +\cos \left( 4\pi y \right)\\ u\left( x,0,t \right) =u\left( x,1,t \right) =0\\ u\left( 0,y,t \right) =u\left( 1,y,t \right) =0\\ \end{array} \right.$

由于完整展现二维热传导需要四维，所以我们只可视化它随时间的动态过程：

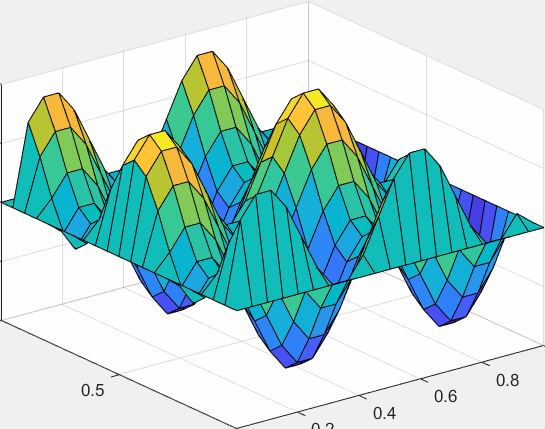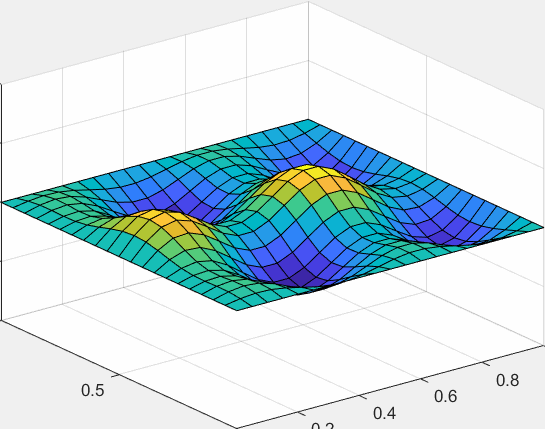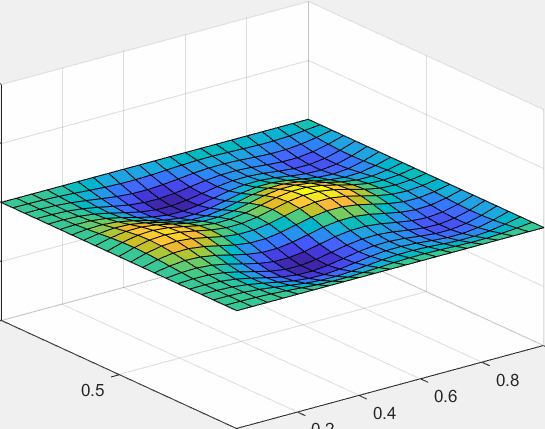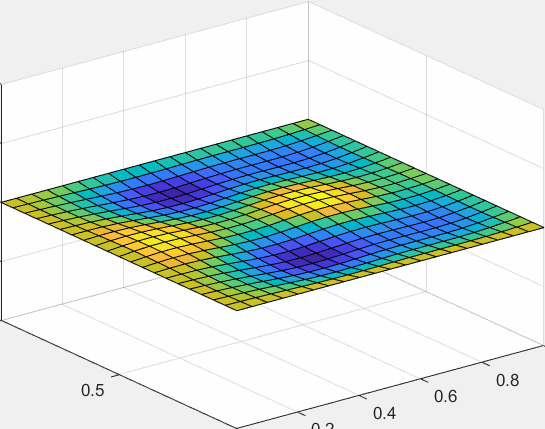
更复杂的情况/PDEtool

上面的两个例子只是很简单的应用，实际上边界条件可能并不像例子里一样是第一类的，并且边界可能是圆，甚至是周期性的；且上面例子的维数不超过二维，当维数为3时，再归结出一套矩阵之间的迭代公式是很麻烦的，如果真的遇到了三维的偏微分问题，建议列出各元素的迭代关系后无脑写$for$循环。

但，如果我们已经知道了某个偏微分方程的全部信息，可以直接用matlab中的PDEtool来进行解方程，这个操作起来相当的简单，只要知道方程的格式，点几个按钮就能得到数值解。

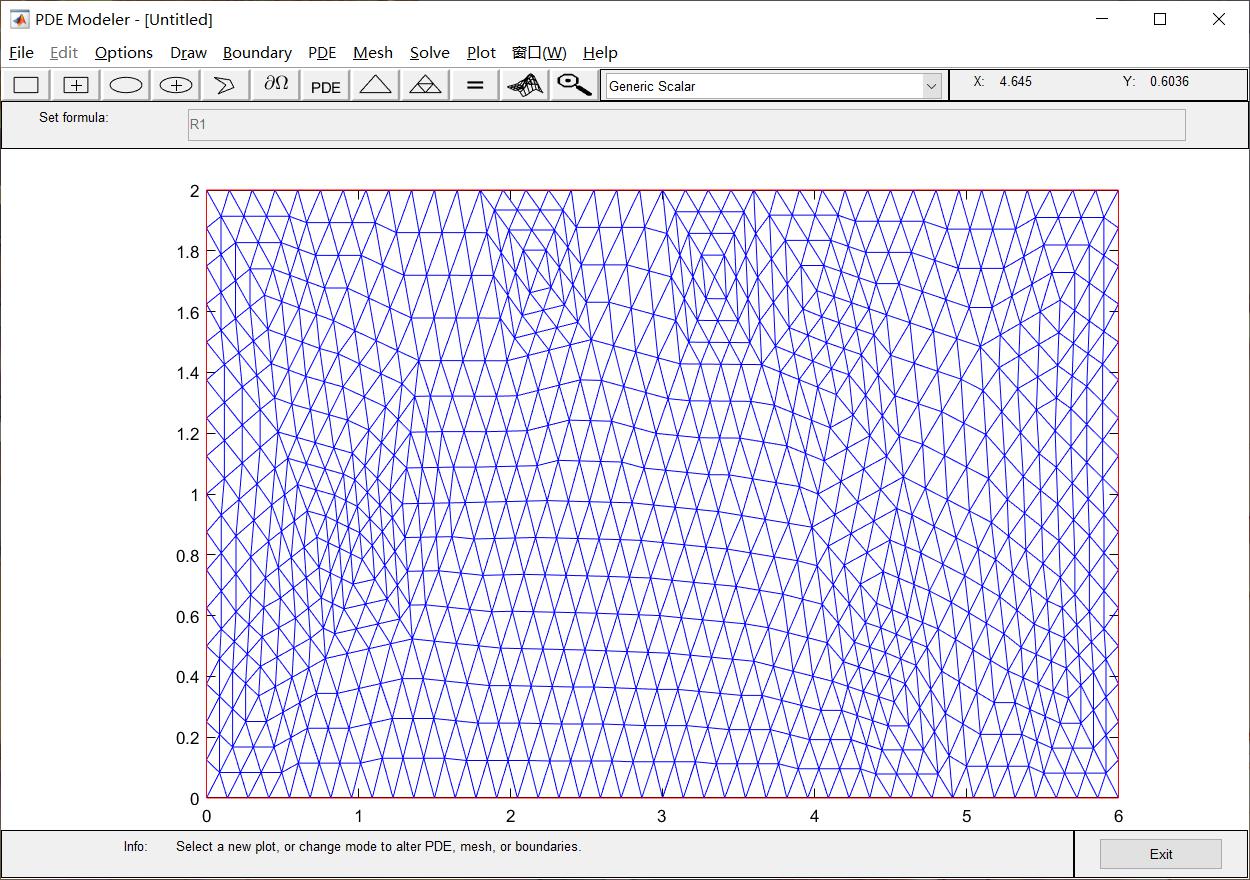
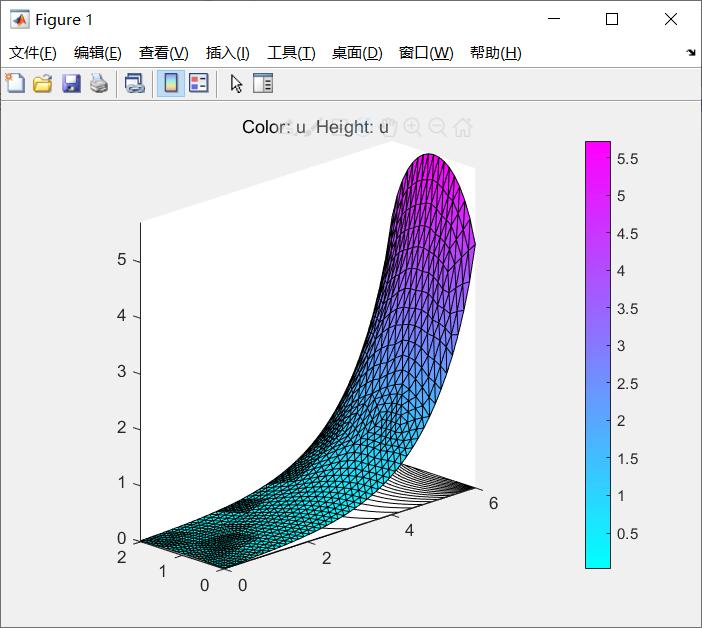
第二类边界条件处理起来稍微复杂一点点，我们以下面的一维抛物线型方程来举个简单的例子：

$\left\{ \begin{array}{c} \frac{\partial u}{\partial t}=\frac{\partial ^2u}{\partial x^2}\\ u\left( x,0 \right) =1\\ u_{x}^{'}\left( 0,t \right) -u\left( 0,t \right) =0\\ u_{x}^{'}\left( 1,t \right) +u\left( 1,t \right) =0\\ \end{array} \right.$

这里与上面第一个例子不同的其实就是边界条件不同，我们离散化这个边界条件，在稍加修改之前的边界条件，之后就和上面的过程一样了：

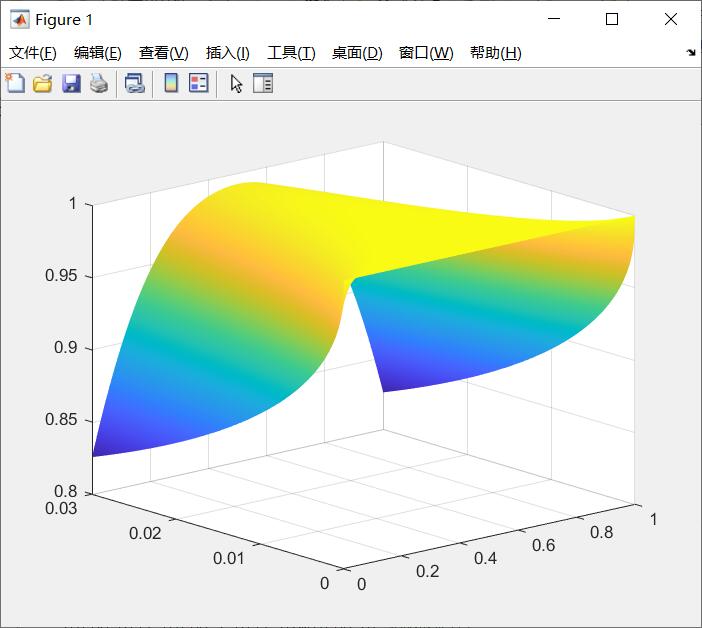
$\left\{ \begin{array}{c} u_{1}^{n}=u_{2}^{n}-\varDelta xu_{1}^{n-1}\\ u_{i_{\max}}^{n}=u_{i_{\max}-1}^{n}-\varDelta xu_{i_{\max}}^{n-1}\\ \end{array} \right.$

现在我们已经可以简单的用数值方法来求解一些偏微分方程了，但是要注意，我们实际上用的都是最简单的差分格式，在调整步长作实验时我们常会遇到一些“奇怪的现象”，这些会在后面介绍不同种差分格式和稳定性时解释到。