偏微分方程

阅读数: 次 2021-07-30

偏微分方程很大程度上扩充了我们描述自然世界的语言，本系列陆续对在数学建模中会用到的偏微分方程知识作一些简单的说明。

下面我先介绍三种在三维情况下常见的偏微分方程来建立对这一体系初步的了解。

实际上由实际意义出发的偏微分方程抽象成下面的式子可能有些跳跃，但他们的来源和推导其实是不难理解的，在这里我就先略去物理层面的推导，我们只需要把偏微分方程视作描述一种现象的语言即可。

椭圆型方程

我们这里只介绍椭圆型方程中常见的泊松(Poisson)方程，存在于反应扩散，电磁场问题中。

在学高等数学的时候，我们曾经被要求算一些很无趣的练习题，例如：

$z=\ln \sqrt{x^2+y^2},u=\frac{1}{\sqrt{x^2+y^2+z^2}}$

我们被要求计算他们二阶偏导数的和，有时会发现他们的和居然是零（或者别的定常数），实际上给出的这些函数就是我们下面要说的偏微分方程的解。

它的形式是：

$\frac{\partial ^2u}{\partial x^2}+\frac{\partial ^2u}{\partial y^2}+\frac{\partial ^2u}{\partial z^2}=f\left( x,y,z \right)$

当$f\left( x,y,z \right)=0 $时，该方程被记作拉普拉斯(Laplace)方程，它的解称为调和函数，同时我们引入拉普拉斯算子来简记这个方程：$\nabla ^2$,顺带一提的是这个记号的意义实际上是对于二阶可微实函数梯度的散度。

抛物线型方程

这类方程是基于热传导建立的简单数学模型，是由能量守恒定律及傅里叶定律推出的。

$\frac{\partial u}{\partial t}=a^2\left( \frac{\partial ^2u}{\partial x^2}+\frac{\partial ^2u}{\partial y^2}+\frac{\partial ^2u}{\partial z^2} \right)$

双曲线型方程

大学物理里见过的波动方程是很常用的双曲线型方程

$\frac{\partial ^2u}{\partial t^2}=a^2\left( \frac{\partial ^2u}{\partial x^2}+\frac{\partial ^2u}{\partial y^2}+\frac{\partial ^2u}{\partial z^2} \right)$

以及对流方程

$\frac{\partial u}{\partial t}=C\left( \frac{\partial u}{\partial x}+\frac{\partial u}{\partial y}+\frac{\partial u}{\partial z} \right)$

上面介绍的只是这些方程的简单形式，实际上在很多情况下，这些方程会有更多的参数，比如当考虑到各向异性时，扩散系数需要由三个不同的参数来表示，等等，值得一提的是，实际上扩散和对流现象两者是密不可分的，但合并后的对流-扩散方程已经远远超出了数学建模的难度，这里就从略了。

边界条件/初始条件

就像求解一阶常系数线性微分方程，我们需要一个初值一样。在这里我们求解偏微分方程也需要一些条件，第一就是初始条件，如初始时温度场的分布函数。这是我们很容易理解的。第二就是我们不太熟悉的边界条件，但它其实有鲜明的意义。

考虑一个在恒温场的铁片的温度分布，它的表面就是一个边界，而这边界的温度与外界的恒温场有关，不止服从于热传导方程。这就是边界条件。例如：

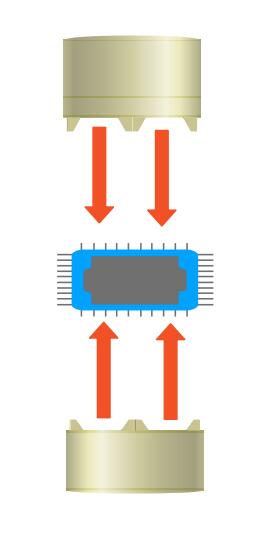
在上面这个烘制电路板的背景下，我们考虑热空气的对称性，将其视作满足一维热传导方程。此时的机理建模即为：

$\left\{ \begin{array}{c} \frac{\partial T}{\partial t}=\alpha \frac{\partial ^2T}{\partial y^2}\\ \frac{\partial T}{\partial y}|_{y=|\frac{d}{2}|}=h\left( T_e-T_s \right)\\ \end{array} \right.$

第二个方程即为这个情景下的边界条件，它实际上要求了热空气和电路板表面服从牛顿冷却定律。

（即左边代表单位时间内交换的热量与温差成正比）

一般而言，边界条件分为三种，

第一种为直接给出未知函数在边界的数值，称为第一类边界条件或狄利克雷(Dirichlet)条件。

第二种为给出未知函数在边界外法线的方向导数，称为第二类边界条件或诺伊曼(Neumann)条件。

第三种为前两种的组合。

但是实际上并不是任何时候都需要有边界条件，比如如果真实的边界足够遥远，那么我们在计算的时候也无需考虑边界条件，这是因具体问题而定的。

现在我们已经了解了简单的偏微分方程的类型，以及边界条件和初始条件，下一篇将介绍如何求解一个偏微分方程。